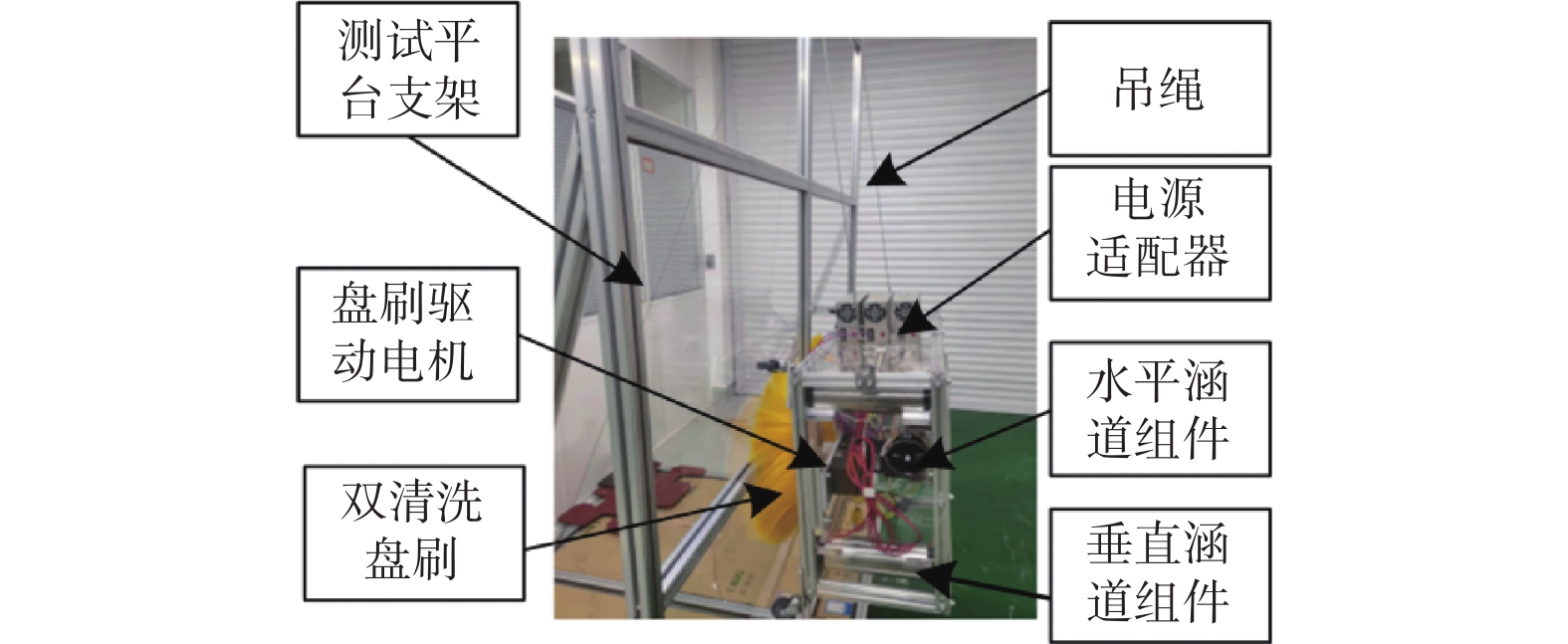
Attitude PID control parameter tuning of curtain wall cleaning robot based on improved genetic algorithm
-
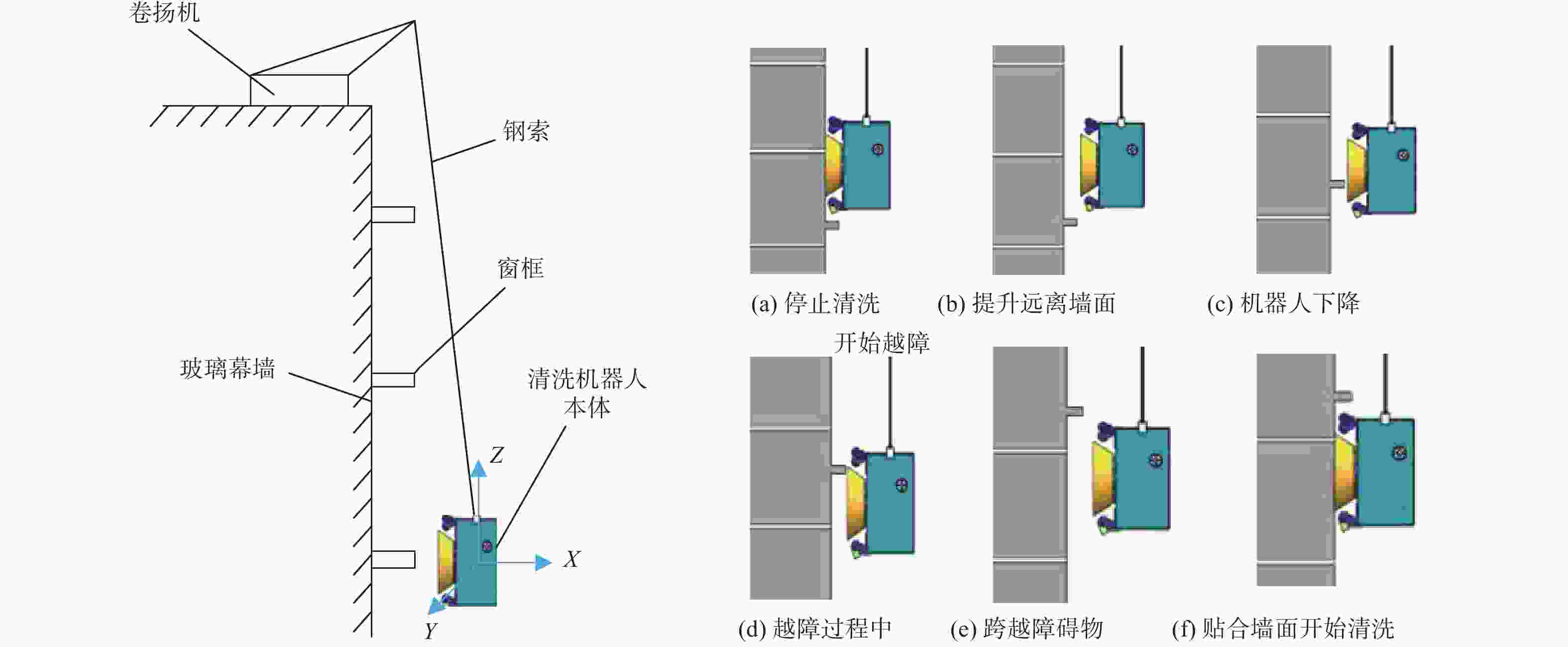
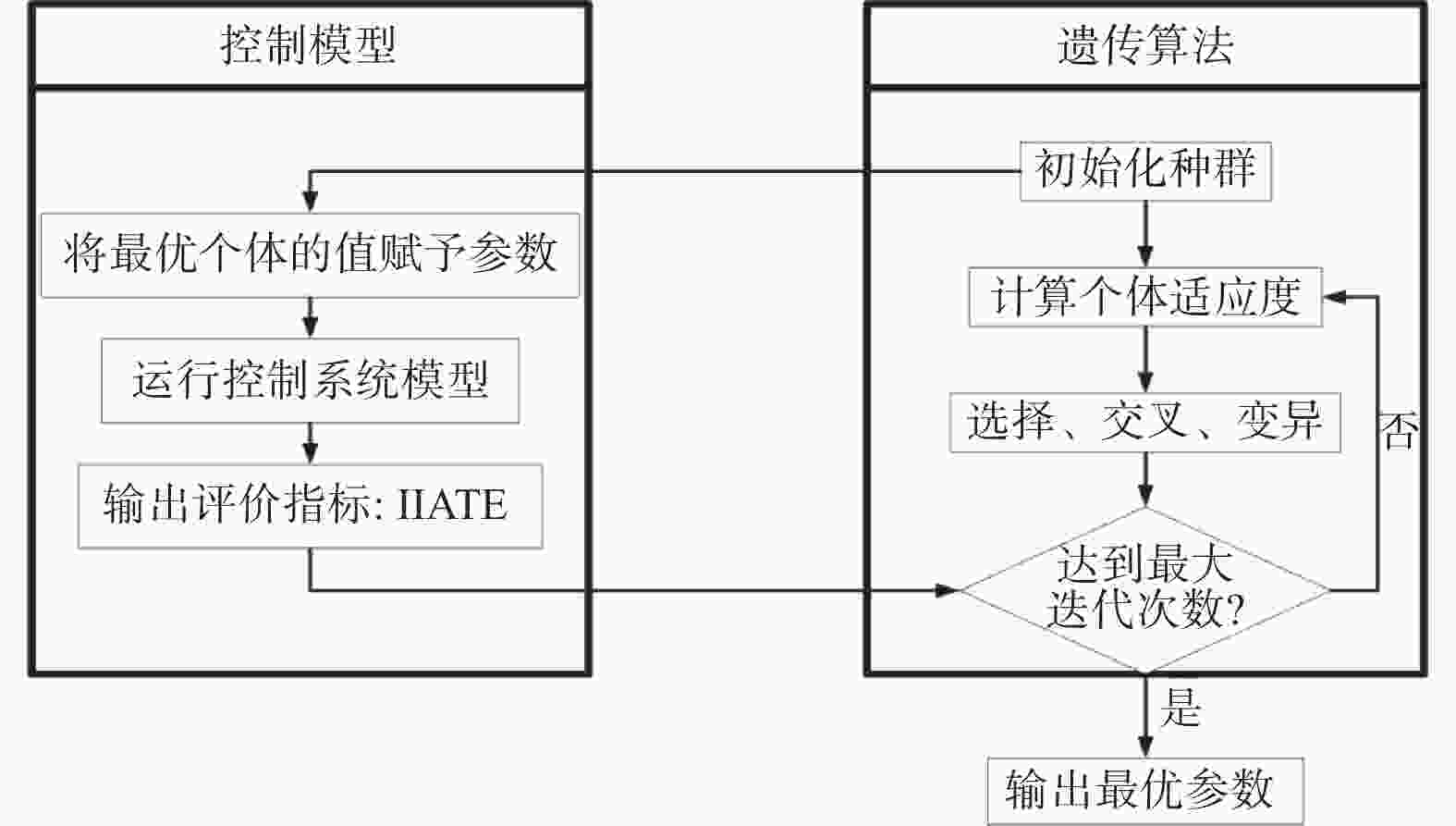
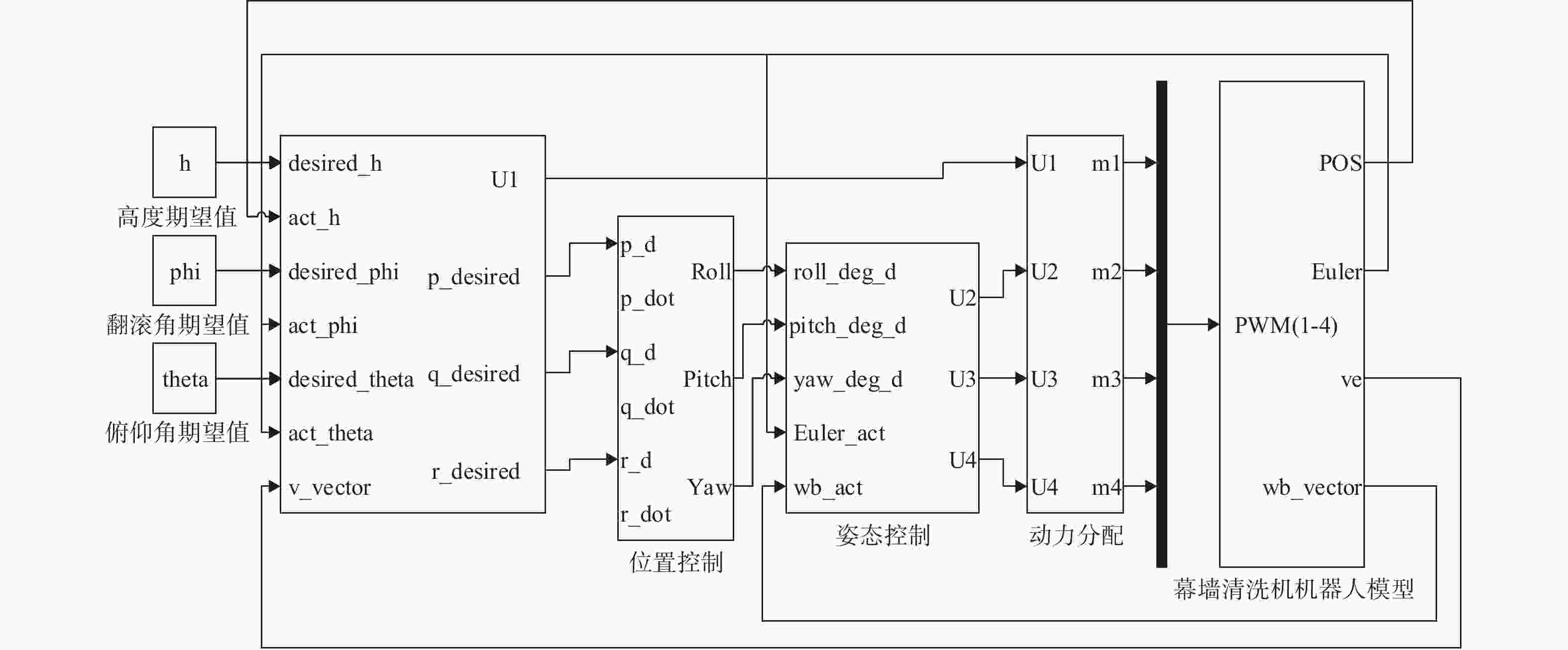
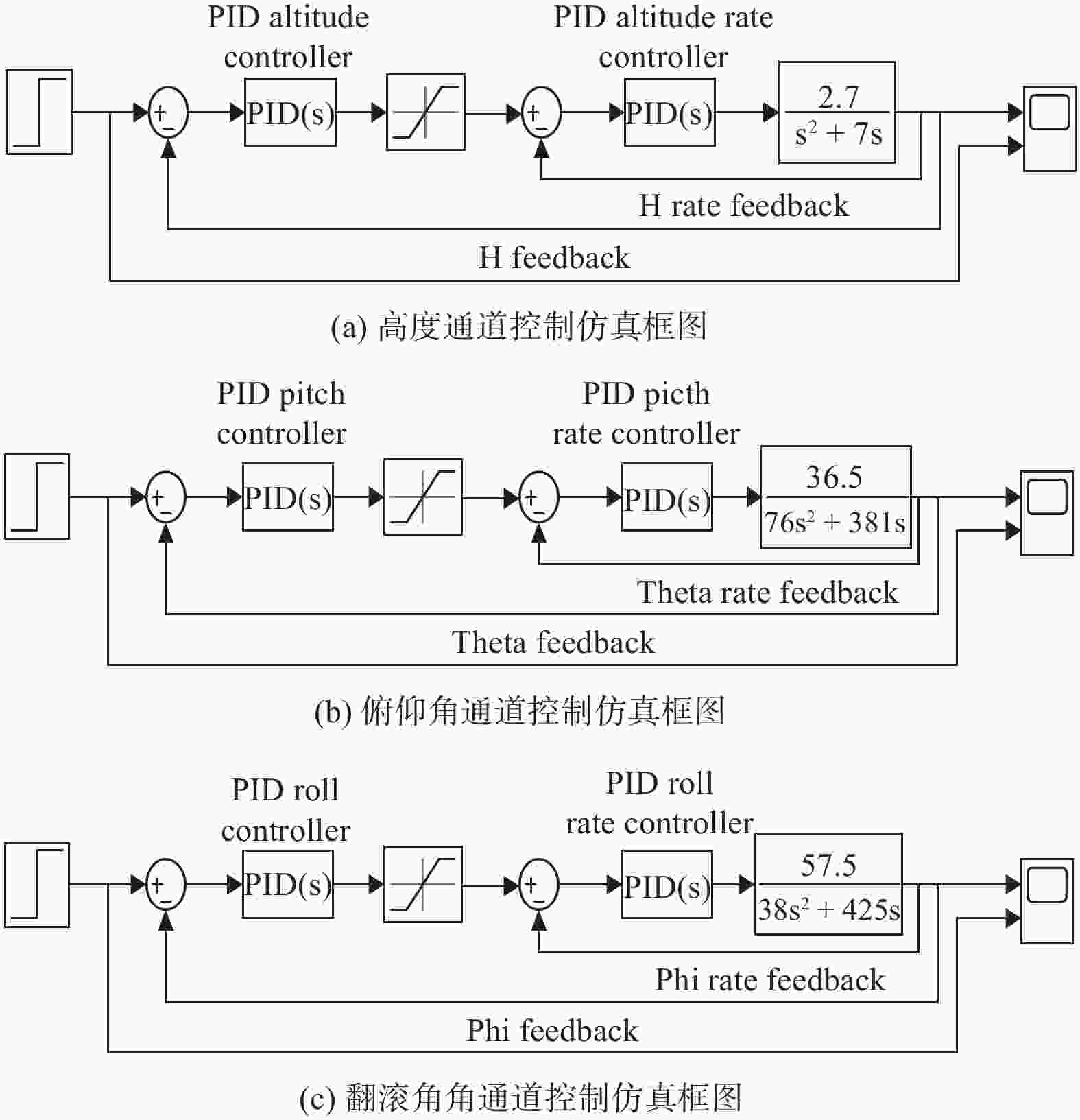
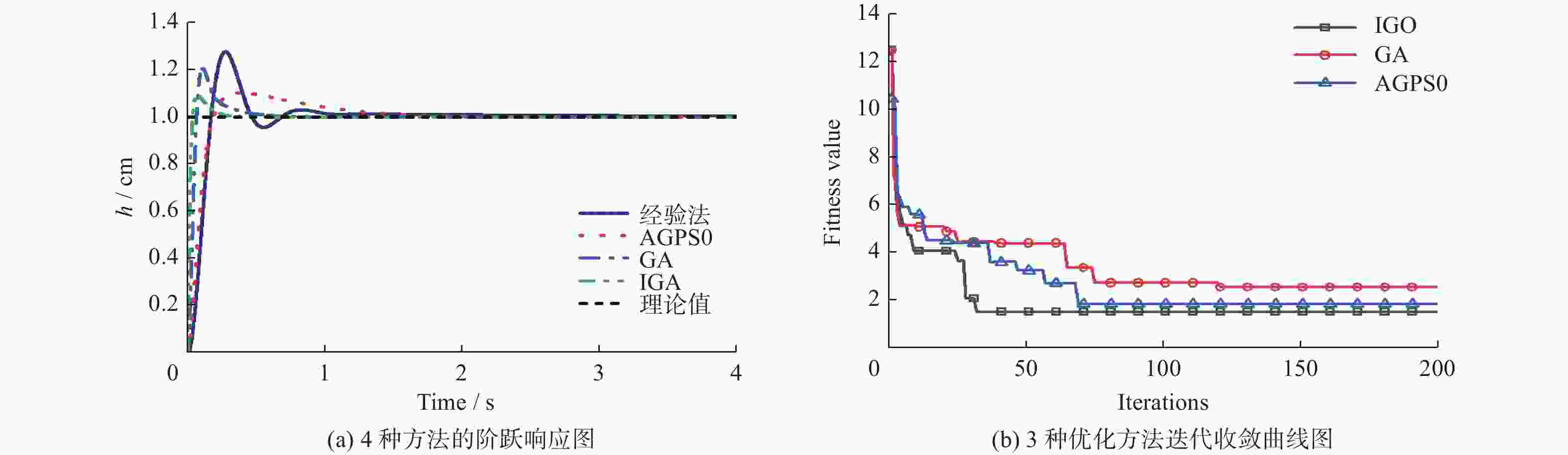
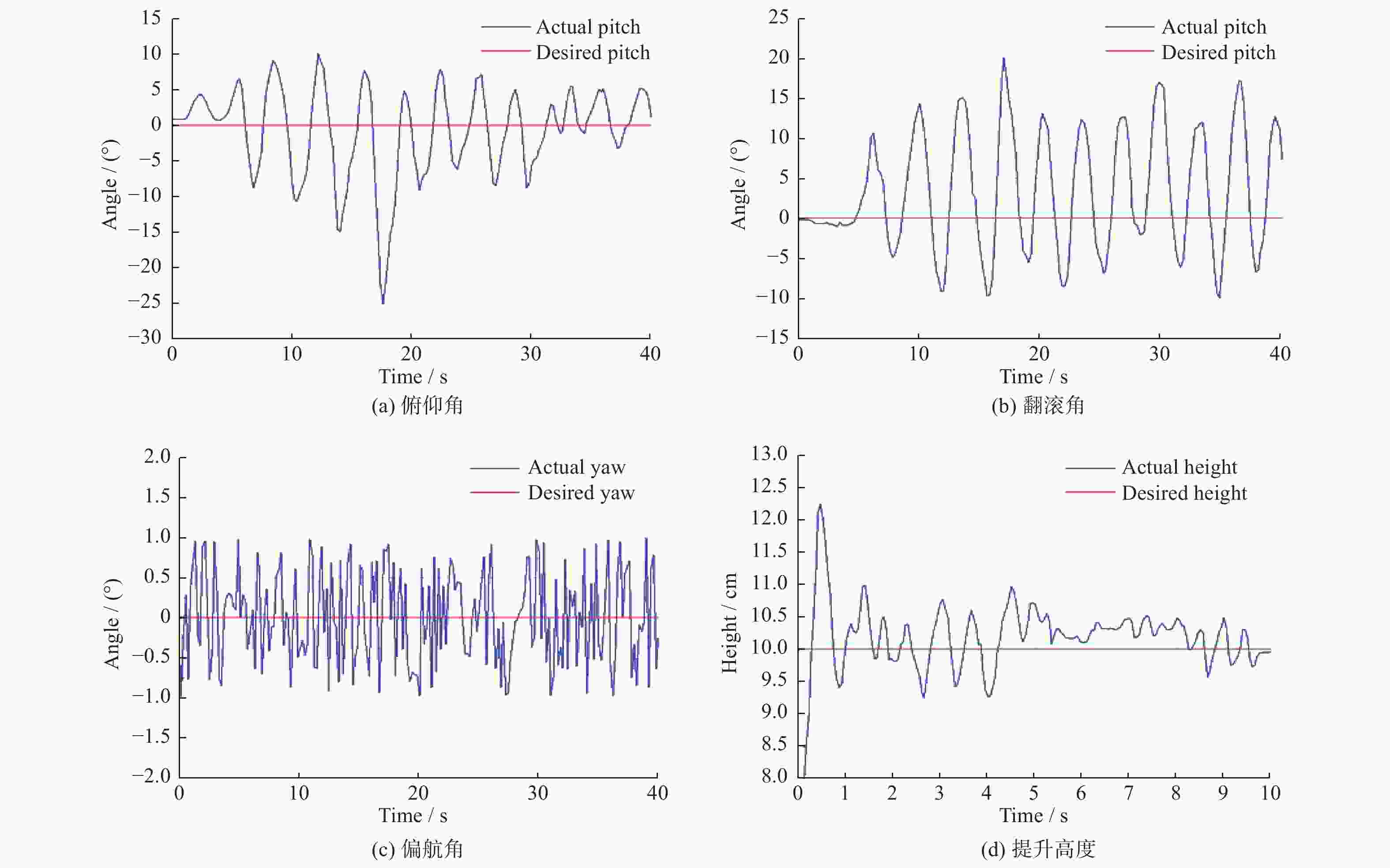
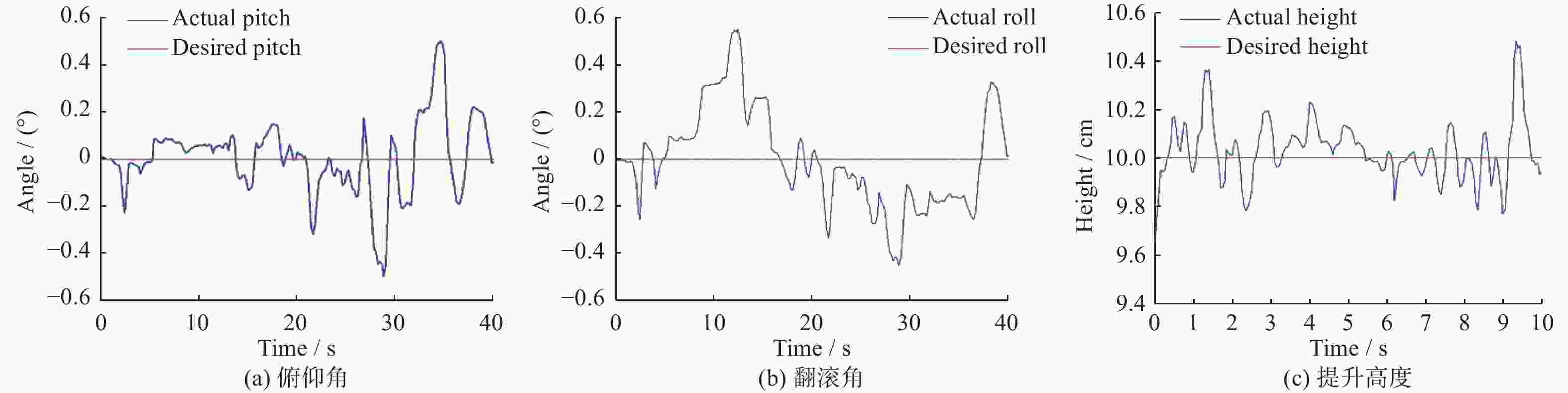
摘要: 针对高楼幕墙清洗机器人姿态PID参数整定耗时长,误差大的问题,提出一种改进遗传算法(improved genetic algorithm, IGA)。引入halton序列作为初始种群,在交叉和变异环节引入自适应动态调节机制,提出综合性能更好的改进时间加权绝对误差积分(improved integral of time-weighted absolute error, IITAE)评价指标函数。使用IGA以及人工经验法、AGPSO算法、GA算法等进行PID参数整定试验,结果表明,IGA算法的整定结果在目标函数值上较其他算法提高20%以上;在收敛时间上降低50%以上。IGA方法设计的控制器能够实现机器人姿态的稳定控制,在幕墙清洗机器人空中姿态的稳定控制方面,具有较好的应用价值。Abstract: To address the problem of time-consuming and large errors in the attitude PID parameter tuning of a high-rise curtain wall cleaning robot, an improved genetic algorithm (IGA) was proposed. The halton sequence was introduced as the initial population, the adaptive dynamic regulation mechanism was introduced in the crossover and variation stages, and improved integral of time-weighted absolute error (IITAE) evaluation index function with better comprehensive performance was proposed. PID parameter tuning experiments were carried out using IGA, manual empirical method, AGPSO and GA. The results show that the tuning results of the IGA algorithm are more than 20% higher than other algorithms in terms of the objective function value and reduced the convergence time by more than 50%. The controller designed by the IGA methodcan achieve stable control of robot attitude, which has good application value for air attitude stability control of curtain wall cleaning robot.
-
Key words:
- curtain wall cleaning robot /
- attitude control /
- PID tuning /
- genetic algorithm (GA)
-
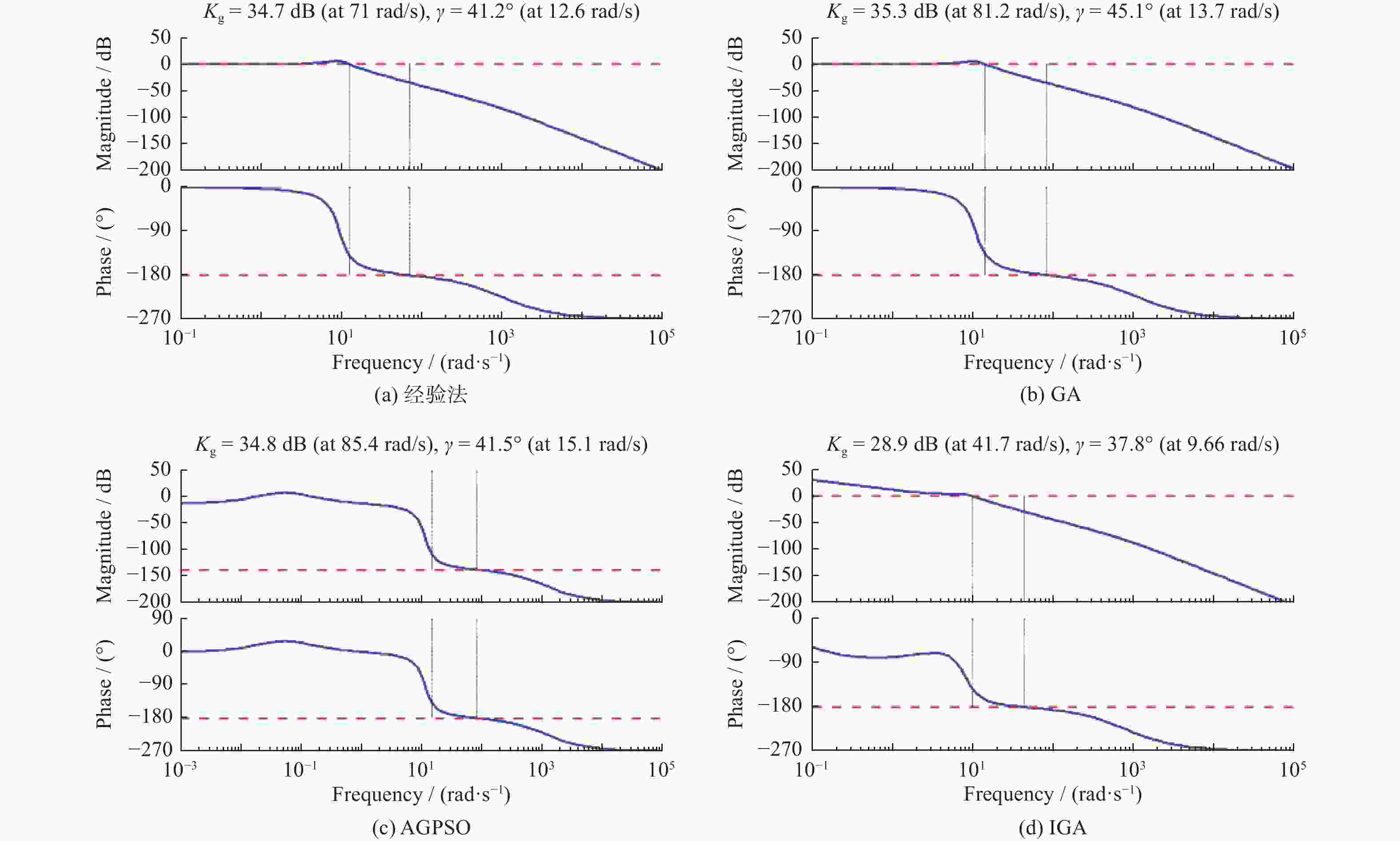
表 1 算法主要参数
Table 1. Main parameters of algorithm
算法 参数 取值 AGPSO 惯性系数最小值ωmin 0.6 惯性系数最大值ωmax 0.9 学习因子C1初始值C1begin 2.2 学习因素C1最终值C1end 0.8 学习因子C2初始值C2begin 0.8 学习因素C2最终值C2end 2.2 GA 交叉概率Pc 0.6 变异概率Pm 0.08 IGA 交叉概率最小值Pcmin 0.5 交叉概率最大值Pcmax 0.9 变异概率最小值Pmmin 0.005 变异概率最大值Pmmax 0.09 表 2 4种方法整定结果
Table 2. Tuning results of four methods
参数 经验法 AGPSO GA IGA Kp1 40 71.7452 52.4645 11.5132 Ki1 2 0.5627 5.7563 2.5258 Kd1 0.01 3.2768 1.4225 0.7854 Kp2 23.5 12.7365 34.5148 23.4314 Ki2 1.23 0.8685 15.4132 1.3391 Kd2 2.1 12.8285 0.2154 5.1437 -
[1] 艾福强, 包建东, 刘正权. 基于粒子群优化模糊PID控制的多足式真空吸附机器人控制方案设计[J] . 电子测量技术,2023,46(2):67 − 72. [2] 徐广红, 陈兵, 杨隆庆, 等. 新型高楼幕墙清洗机器人的研制及安全性分析[J] . 机械设计与制造,2017(2):258 − 262. doi: 10.3969/j.issn.1001-3997.2017.02.070 [3] 张晓婷, 李徳镇, 梁仁旺, 等. 挖掘机铲斗电液伺服改进PSO-PID参数整定位置控制[J] . 机械设计与制造,2023(9):181 − 184. doi: 10.3969/j.issn.1001-3997.2023.09.040 [4] 宋英杰, 王刚, 唐武生, 等. 基于模糊自适应串级PID控制器的仿生机器鱼位姿控制[J] . 控制工程,2023,30(10):1870 − 1880. [5] 吕红芳, 王涛, 嵇月强, 等. 基于免疫粒子群算法的PID参数优化研究[J] . 中国工程机械学报,2022,20(3):194 − 198. doi: 10.3969/j.issn.1672-5581.2022.3.zggcjxxb202203002 [6] 冯浩, 姜金叶, 宋倩玉, 等. 电液伺服系统多PID控制器参数整定优化[J/OL] . 控制理论与应用: 1-5. (2023-10-08)[2024-1-08] . http://kns.cnki.net/kcms/detail/44.1240.tp.20230928.1132.088.html. [7] XU W, YUE X, YIN S, et al. Research on pid parameter tuning method of brushless DC motor with itae index[C] //Proceedings of 2023 IEEE 6th Information Technology, Networking, Electronic and Automation Control Conference(ITNEC). Chongqing: IEEE, 2023: 177−180. [8] SHI P. PID parameter tuning based on improved particle swarm optimization algorithm[C] //Proceedings of 2023 3rd International Conference on Electrical Engineering and Computer Technology. Nanjing: IOP Publishing, 2023. [9] 李盛前, 张小帆. 基于免疫粒子群的机器人自抗扰控制器参数整定方法[J] . 机床与液压,2023, 51(14): 63−68. doi: 10.3969/j.issn.1001-3881.2023.14.011 [10] 李昆, 赵理, 汪光, 等. 基于适应度继承的航空发电机比例-积分-微分参数优化算法[J] . 科学技术与工程,2021,21(33):14258 − 14265. doi: 10.3969/j.issn.1671-1815.2021.33.031 [11] PRATA B, BASANTA P, KRISHNA Y P, et al. Application of particle swarm optimization (PSO) algorithm for PID parameter tuning in speed control of brushless DC (BLDC) motor[J] . Journal of Physics: Conference Series,2023,2570(1):012018. [12] HU Z F, LIU Y J, HE Y L, et al. Fuzzy PID control of the three-degree-of-freedom parallel mech- anism based on genetic algorithm[J] . Applied Sciences,2022,12(21):11128. [13] 周向阳, 时延君. 惯性稳定平台单神经元PID自适应复合控制与参数优化[J] . 仪器仪表学报,2019,40(11):189 − 196. [14] 吴振龙, 张灿, 刘艳红. 基于多目标遗传算法的四旋翼飞行器PID设计[EB/OL] . (2023-11-24)[2024-01-08] . https://doi.org/10.14107/j.cnki.kzgc.20220390. [15] 刘建娟, 吴豪然, 姬淼鑫, 等. 多策略改进粒子群优化AGV模糊PID控制[EB/OL] . (2023-11-03)[2024-01-08] . http://kns.cnki.net/kcms/detail/44.1259.TH.20231103.1132.004.html. [16] 梁杰, 专祥涛, 严家政. 基于深度强化学习TD3的PID参数自整定算法[EB/OL] . (2023-04-13)[2024-01-08] . http://kns.cnki.net/kcms/detail/42.1675.T.20230412.1609.002.html. [17] KRÖMER P, PLATOŠ J, SNÁŠEL V. Differential evolution for the optimization of low-discre -pancy generalized halton sequences[J] . Swarm and Evolutionary Computation,2020,54:100649. doi: 10.1016/j.swevo.2020.100649 [18] MMAHADEVA R, KUMAR M, PATHOLE S P, et al. PID control design using AGPSO technique and its application in TITO reverse osmosis desalination plant[J] . IEEE Access,2022,10:125881 − 125892. doi: 10.1109/ACCESS.2022.3224127 -





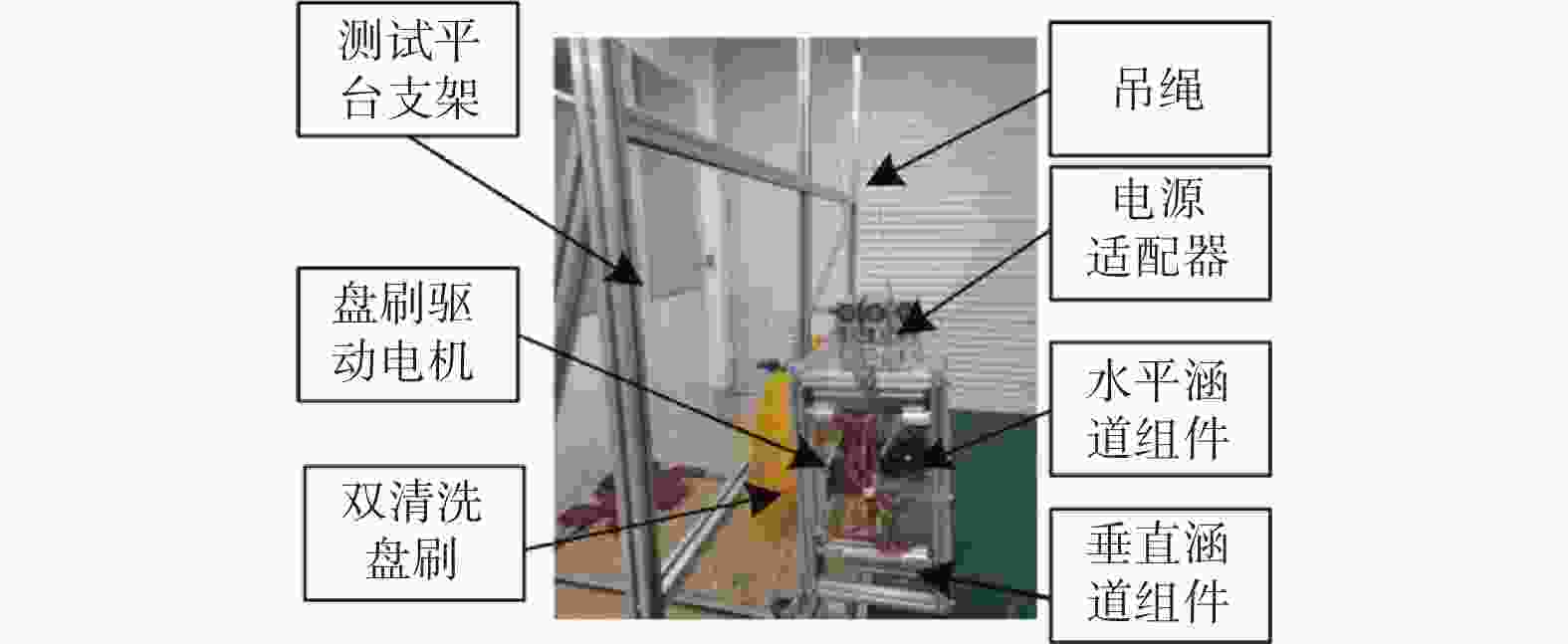
 下载:
下载: