AGV scheduling for order-driven intelligent workshop based on reinforcement learning
-
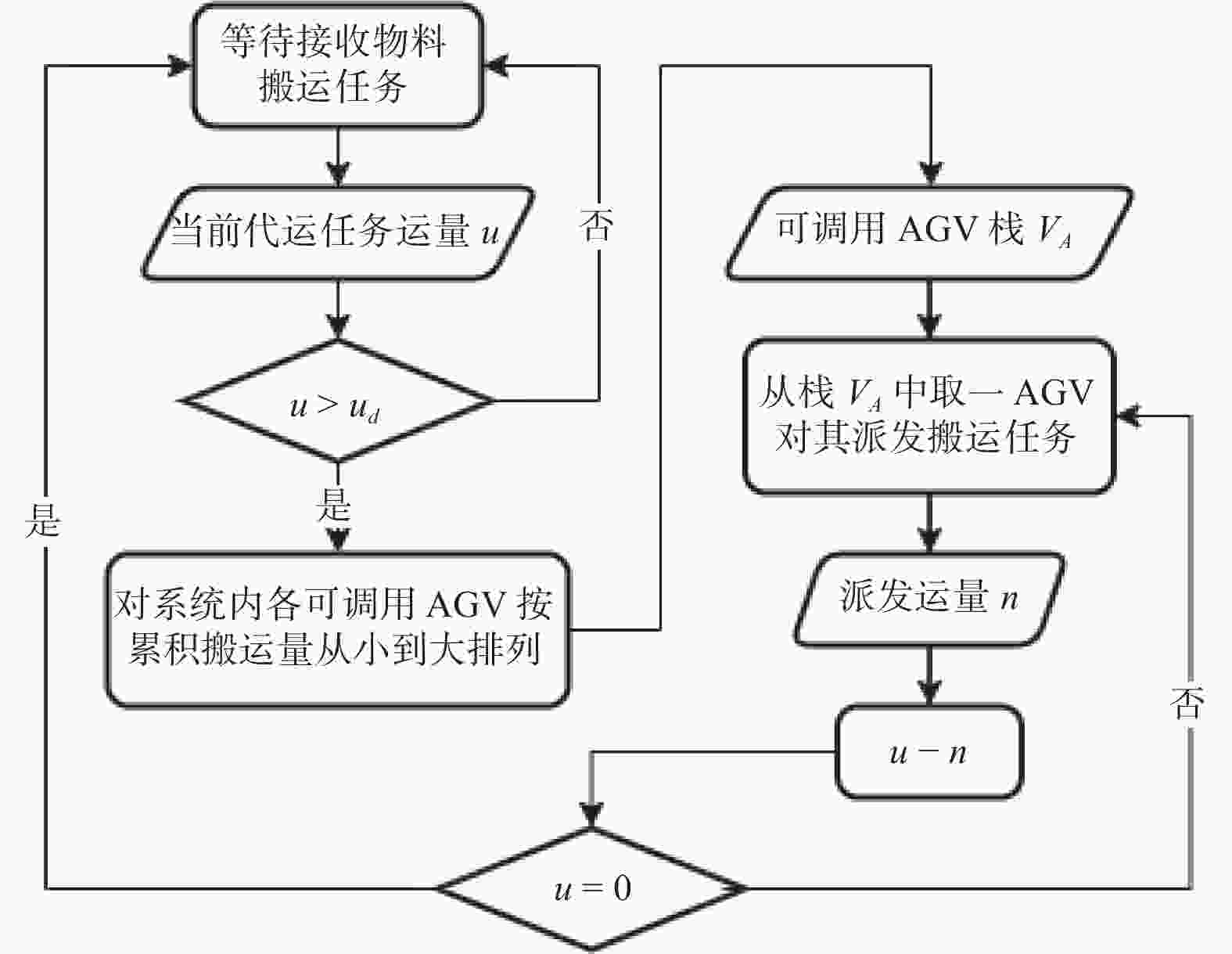
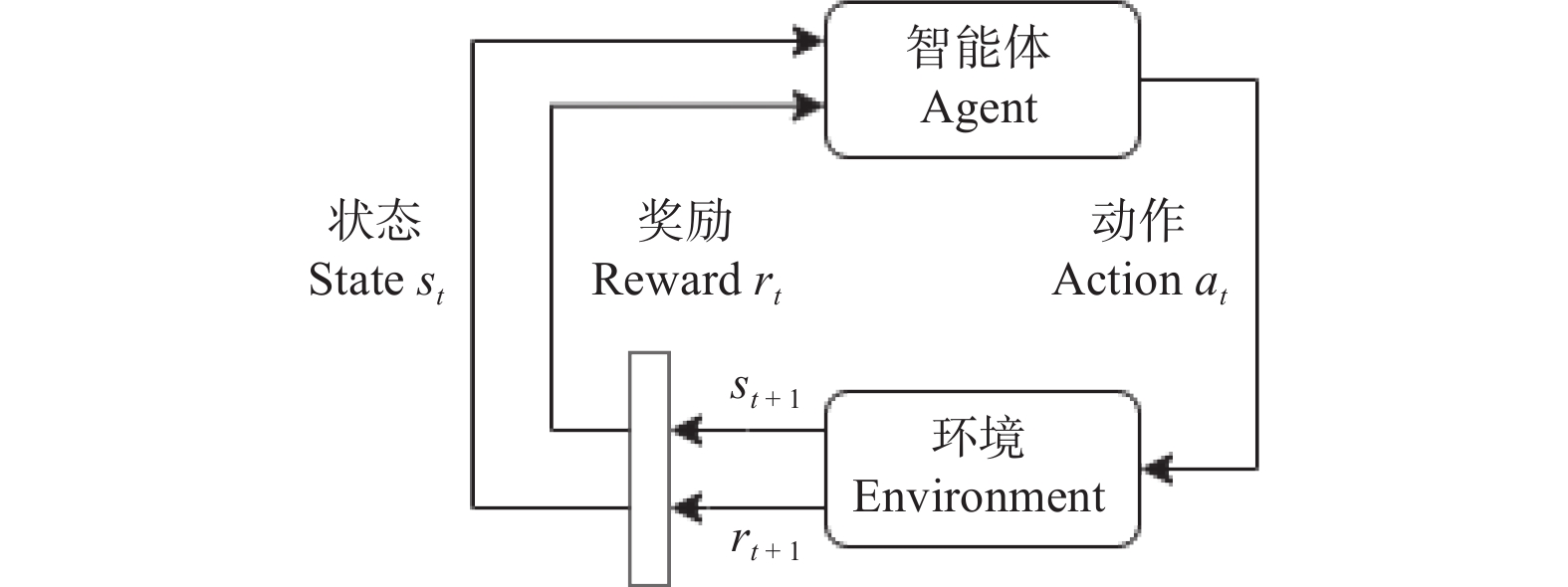
摘要: 物料搬运效率对智能车间的生产调度效率有着重要影响. 物料搬运任务通常由自动导引车(Automated Guided Vehicle,AGV)执行,其具有数量多、任务需求实时变化、任务下达密集等特点. 为及时、高效、准确地处理AGV搬运作业,提出基于强化学习的订单驱动下智能车间AGV调度模型,使用二级调度机制,第一级以负载均衡为目标,基于规则的调度方法对AGV进行任务分配;第二级运用强化学习深度Q网络(Deep Q-Network,DQN)算法对AGV进行单智能体下的搬运路径规划,通过减少智能体动作空间维数的方式,降低调度算法的收敛难度,并通过仿真实例验证该方法的有效性和创新性.Abstract: Material transporting efficiency has an important impact on the production scheduling efficiency of the intelligent workshop. Material transporting tasks are usually executed by automated guided vehicle (AGV), which have large number of tasks, real-time changes in task demand, and intensive task issuance. In order to make the AGV workflow timely, efficient and accurate, an reinforcement-learning-based AGVs' scheduling model was established with a two-level mechanism. The first level aimes for load balancing, and assigns the tasks to AGVs in a rule-based scheduling method. The second level plans each AGV's path by a reinforcement learning deep Q-network (DQN) algorithm with single agent, which can reduce the convergence difficulty of the scheduling algorithm by reducing the dimensions of the agent's action space. The effectiveness and innovation of the method was verified through simulation examples.
-
表 1 状态编码
Table 1. State encoding
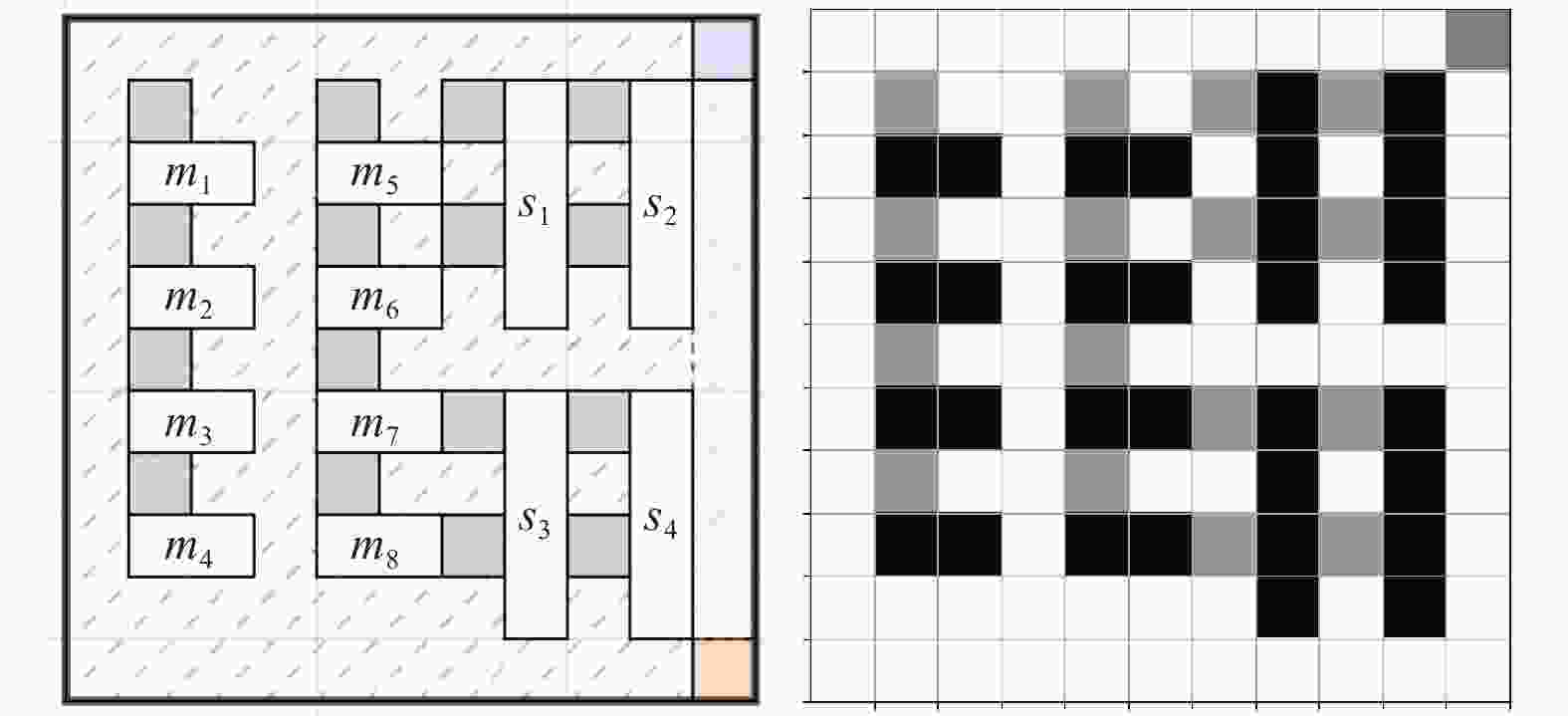
栅格单元状态 栅格单元类型 $ s $值 AGV当前所在 $ N,S,L\cap {g}_{ij}\notin T $ $ 0.5 $ 可通行 $ N,S,L\cap {g}_{ij}\notin T $ $ 1 $ 不可通行 $ W,P $ $ 0 $ 中间目标点 $ L\cap {g}_{ij}\in T $ $0.7 - \dfrac{0.3}{n-1}j$ 终点 $ E $ $ 0.3 $ 表 2 奖励函数
Table 2. Reward function
状况 奖励$ r $ 执行有效移动指令 $-\dfrac{1}{m \times n}$ 下达无效移动指令 $- \dfrac{4}{ \sqrt{m \times n} }$ 到达目标装卸点 $\dfrac{1}{n_T}$ 完成搬运任务后到达回收点 $ 1 $ 表 3 某次决策点的搬运任务分配
Table 3. Material transport tasks assigned on one decision point
待运量 轮次 选定AGV 当前状态 当轮运量 累积运量 搬运任务集$ T $ $ 12 $ 01 $ {v}_{1} $ 可用 $ 4 $ $ 22\to 26 $ $ {T}_{1}=\left\{\left(\left(3, 6\right), (0, 2), 1\right),\left(\left(1, 1\right), (2, 2), 2\right),\left(\left(7, 1\right), (2, 0), 3\right)\right\} $ 8 02 $ {v}_{2} $ 可用 2 $ 24\to 26 $ $ {T}_{2}=\left\{\left(\left(3, 4\right), (0,1), 1\right),\left(\left(5, 4\right), (0, 1), 1\right),\left(\left(6, 8\right), (2, 0), 2\right)\right\} $ 6 03 $ {v}_{3} $ 充电 0 $ 28\to 28 $ 无 6 04 $ {v}_{1} $ 可用 2 $ 26\to 28 $ $ {T}_{4} = \left\{ \left( \left( 3, 6 \right), (0, 2) , 1\right), \left(\left(3, 1\right), (1, 0), 2 \right), (\left(7, 4\right), (1,0) , 2) \right\} $ 4 05 $ {v}_{2} $ 可用 4 $ 26\to 30 $ $ {T}_{5}=\left\{\left(\left(5, 1\right), (0, 4), 1 \right),\left(\left(5, 4\right), (2,0), 2\right),\left(\left(1, 8\right), (2,0) , 2\right)\right\} $ -
[1] CHAUDHRY I A, KHAN A A. A research survey: Review of flexible job shop scheduling techniques[J] . International Transactions in Operational Research,2016,23(3):551 − 591. doi: 10.1111/itor.12199 [2] FRANCOIS-LAVET V, HENDERSON P. An Introduction to deep reinforcement learning[J] . Foundations and Trends in Machine Learning,2018,11(3/4):219 − 354. doi: 10.1561/2200000071 [3] 肖蒙. 考虑物料搬运的离散制造车间多资源调度[D]. 上海: 东华大学, 2022. [4] YU J L, SU Y C, LIAO Y F. The path planning of mobile robot by neural networks and hierarchical reinforcement learning[J] . Frontiers in Neurorobotics,2020,14:63. doi: 10.3389/fnbot.2020.00063 [5] SOONG L E, PAULINE O, CHUN C K. Solving the optimal path planning of a mobile robot using improved Q-learning[J] . Robotics and Autonomous Systems,2019,115(3):143 − 161. [6] LIU Z X, WANG Q C, YANG B S. Reinforcement learning-based path planning algorithm for mobile robots[J] . Wireless Communications and Mobile Computing,2022,2022:1 − 10. [7] 刘辉, 肖克, 王京擘. 基于多智能体强化学习的多AGV 路径规划方法[J] . 自动化与仪表,2020,35(2):84 − 89. [8] 宋博伟. 基于强化学习的混流车间AGV路径规划研究[D]. 沈阳: 沈阳大学, 2021. [9] 寇晨光. 订单驱动的型材车间天车智能调度研究[D]. 哈尔滨: 哈尔滨理工大学, 2018. [10] 陈赐. 基于机器学习的多载量小车实时调度方法研究[D]. 上海: 上海交通大学, 2014. [11] 王慧, 秦广义, 杨春梅. 定制家具板材搬运AGV路径规划[J] . 包装工程,2021,42(17):203 − 209. [12] 熊俊涛, 李中行, 陈淑绵, 等. 基于深度强化学习的虚拟机器人采摘路径避障规划[J] . 农业机械学报,2020,51(S2):1 − 10. [13] 杨海兰, 祁永强, 吴保磊, 等. 动态环境下基于忆阻强化学习的移动机器人路径规划[J] . 系统仿真学报,2023,35(7):1619 − 1633. -





 下载:
下载: