Prediction method of bearing remaining useful life based on CNN and attention BiLSTM
-
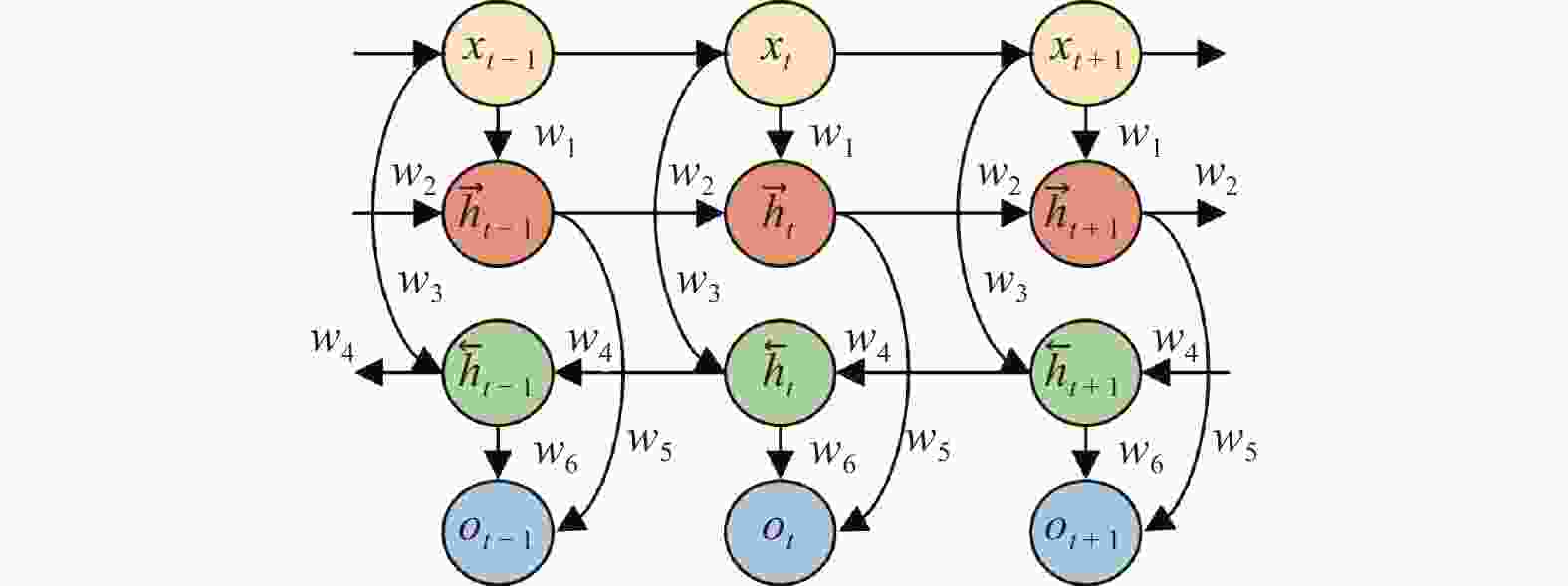
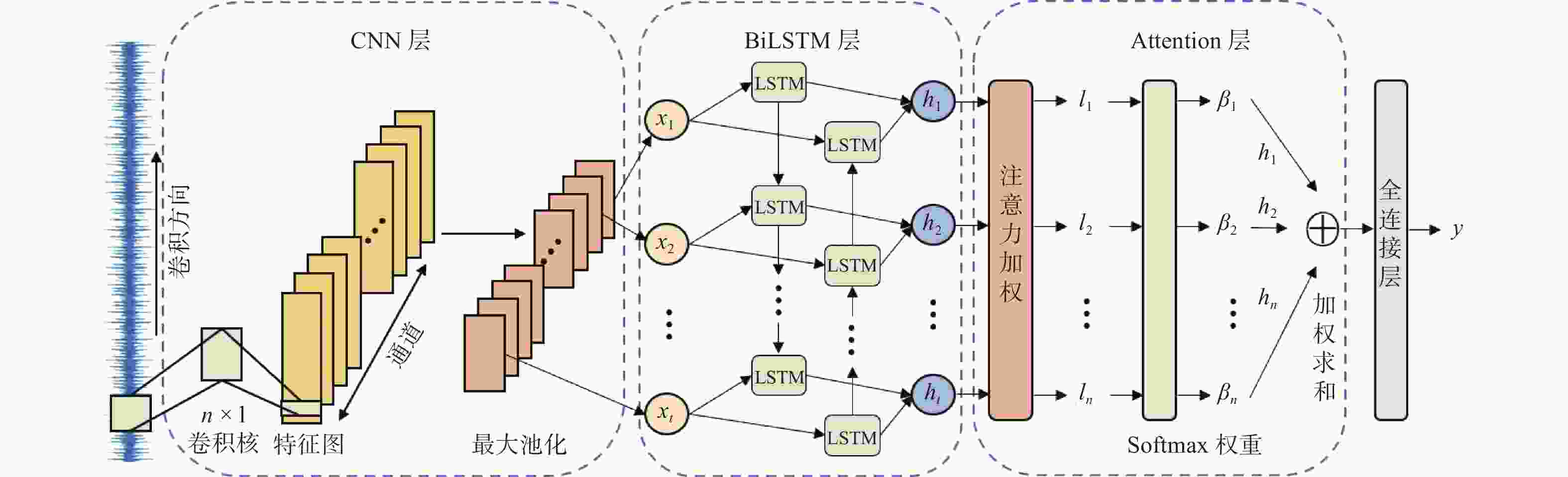
摘要: 滚动轴承的剩余使用寿命(Remaining Useful Life,RUL)预测对于旋转机械的运行和维护具有重要意义. 以卷积神经网络(Convolutional Neural Network,CNN)为代表的深度学习方法虽然可以从轴承振动信号中自动提取特征,却不能对特征进行自适应的选择以提高模型对重要特征的关注程度. 针对上述问题,提出一种基于CNN和注意力双向长短期记忆网络(Bidirectional Long Short-Term Memory,BiLSTM)的轴承RUL预测方法. 首先通过CNN对振动信号进行空间特征提取;然后利用BiLSTM提取时序特征;接着利用注意力机制增强模型对重要特征的关注程度,并以全连接层作为解码器预测健康指标(Health Indicator,HI);最后利用加权平均法对HI预测值进行修正,并利用多项式拟合曲线进行RUL预测. 结果表明, 所提方法的绝对百分比误差比卷积长短期记忆网络(CNN-LSTM)低14.36%,比传统的自组织映射网络(SOM)低21.28%,可用于多故障模式下的RUL预测.Abstract: The remaining useful life (RUL) prediction of rolling bearings is of great significance for the operation and maintenance of rotating machinery. Although the deep learning method represented by convolutional neural network (CNN) can automatically extract features from bearing vibration signals, it can not adaptively select features to improve the attention of the model to important features. In response to the above problems, a bearing RUL prediction method based on CNN and attention bidirectional long short-term memory (BiLSTM) was proposed. Firstly, the spatial features of vibration signals were extracted by CNN, the temporal features were extracted by BiLSTM. Then, the attention mechanism was used to enhance the attention of the model to important features, and the full connection layer was used as the decoder to predict the health indicator (HI). Finally, the weighted average method was used to modify the HI prediction value, and the polynomial fitting curve was used for RUL prediction. The results show that the absolute percentage error of the proposed method is 14.36% lower than that of convolutional long short-term memory (CNN-LSTM) and 21.28% lower than that of traditional self-organizing map network (SOM), which can be effectively used for RUL prediction in multiple fault modes.
-
表 1 数据集情况
Table 1. Data sets situation
工况 转速/(r·min-1) 负载/N 训练数据集 测试数据集 工况1 1800 4000 Bearing1_1、Bearing1_2 Bearing1_3、Bearing1_4、Bearing1_5、Bearing1_6、、Bearing1_7 工况2 1650 4200 Bearing2_1、Bearing2_2 Bearing2_3、Bearing2_4、Bearing2_5、Bearing2_6、、Bearing2_7 工况3 1500 5000 Bearing3_1、Bearing3_2 Bearing3_3 表 2 模型结构参数
Table 2. Model structure parameters
序号 层类型 关键参数 输出 0 输入层 — 1280×1 1 卷积层 核大小:16×1,通道数:10,步长:4 320×10 2 池化层 核大小:2×1,步长:2 160×10 3 卷积层 核大小:4×1,通道数:20,步长:2 80×20 4 池化层 核大小:2×1,步长:2 40×20 5 BiLSTM层 LSTM单元数:128,
激活函数:tanh,dropout:0.3256×20 6 BiLSTM层 LSTM单元数:128,
激活函数:tanh,dropout:0.3256×20 7 Attention层 — 256×1 8 全连接层 — 1 表 3 RUL预测结果
Table 3. RUL prediction results
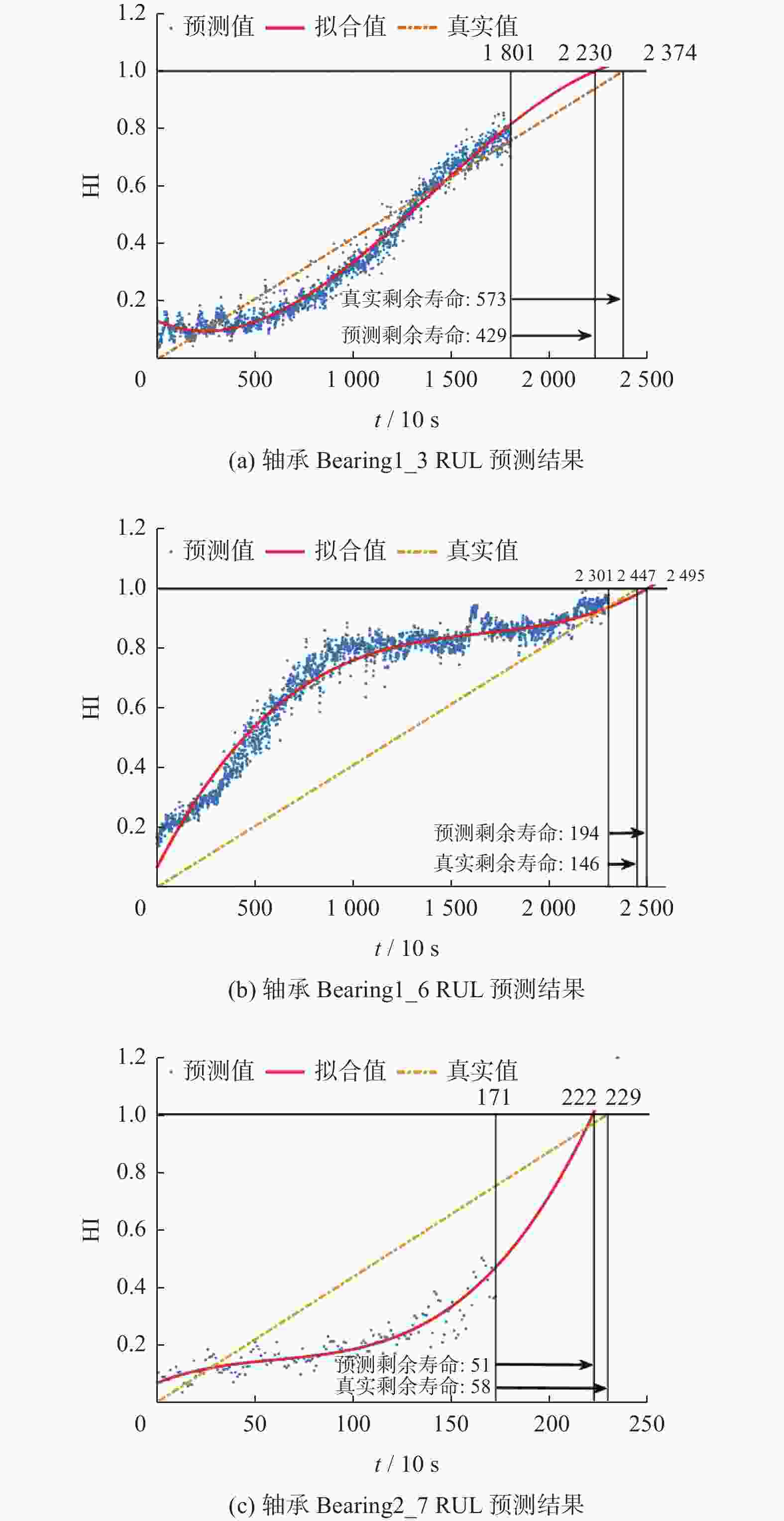
轴承 当前时刻/
(10 s)RUL真实值/
(10 s)RUL预测值/
(10 s)百分比
误差/%文献[17]
结果/%文献[12]
结果/%Bearing1_3 1801 573 429 25.13 54.73 −31.76 Bearing1_4 1138 290 389 −34.14 38.69 62.76 Bearing1_5 2301 161 244 −51.55 −99.40 −136.03 Bearing1_6 2301 146 194 −32.88 −120.07 −32.88 Bearing1_7 1501 757 685 9.51 70.65 −11.09 Bearing2_3 1201 753 349 53.65 75.53 44.22 Bearing2_4 611 139 202 −45.32 19.81 −55.40 Bearing2_5 2001 309 403 −30.42 8.20 68.61 Bearing2_6 571 129 111 13.95 17.87 −51.49 Bearing2_7 171 58 51 12.07 1.69 −68.97 Bearing3_3 351 82 91 −10.98 2.93 −21.96 $|\overline {{\rm{Er}}} |$ 31.96 46.32 53.24 -
[1] 张小丽, 王保建, 马猛, 等. 滚动轴承寿命预测综述[J] . 机械设计与制造,2015(10):221 − 224. doi: 10.3969/j.issn.1001-3997.2015.08.059 [2] 范强飞, 廖爱华, 丁亚琦. 基于RVM和WPHM的滚动轴承剩余寿命预测[J] . 上海工程技术大学学报,2019,33(4):334 − 338. doi: 10.3969/j.issn.1009-444X.2019.04.007 [3] WANG Y, PENG Y Z, ZI Y Y, et al. A two-stage data-driven-based prognostic approach for bearing degradation problem[J] . IEEE Transactions on Industrial Informatics,2016,12(3):924 − 932. doi: 10.1109/TII.2016.2535368 [4] ZHANG Z, WANG Y, WANG K. Fault diagnosis and prognosis using wavelet packet decomposition, fourier transform and artificial neural network[J] . Journal of Intelligent Manufacturing,2013,24(6):1213 − 1227. doi: 10.1007/s10845-012-0657-2 [5] CAO L X, QIAN Z, PEI Y . Remaining useful life prediction of wind turbine generator bearing based on EMD with an indicator[C]//Proceedings of 2018 Prognostics and System Health Management Conference. Chongqing: IEEE, 2018: 375 − 379. [6] HUANG H Z, WANG H K, LI Y F, et al. Support vector machine based estimation of remaining useful life: Current research status and future trends[J] . Journal of Mechanical Science and Technology,2015,29(1):151 − 163. doi: 10.1007/s12206-014-1222-z [7] BASTAMI A R, AASI A, ARGHAND H A. Estimation of remaining useful life of rolling element bearings using wavelet packet decomposition and artificial neural network[J] . Iranian Journal of Science and Technology, Transactions of Electrical Engineering,2019,43(S1):233 − 245. [8] WU T, GAO C X, FU Z Y. Prediction of remaining life of rolling bearing based on optimized EEMD[C]//Proceedings of 2018 Chinese Intelligent Systems Conference. Singapore: Springer, 2018: 223 − 230. [9] 张焱, 汤宝平, 韩延, 等. 融合失效样本与截尾样本的滚动轴承寿命预测[J] . 振动与冲击,2017,36(23):17 − 23. [10] CHAUHAN S, YADAV P, TIWARI P, et al. Performance prediction of rolling element bearing with utilization of support vector regression[C]// Proceedings of Reliability, Safety and Hazard Assessment for Risk-Based Technologies. Singapore: Springer, 2020: 535 − 543. [11] WU Q H, FENG Y, HUANG B Q. RUL Prediction of bearings based on mixture of gaussians bayesian belief network and support vector data description[C]//Proceedings of AsiaSim 2016, SCS AutumnSim 2016: Theory, Methodology, Tools and Applications for Modeling and Simulation of Complex Systems. Singapore: Springer, 2016: 118 − 130. [12] HONG S, ZHOU Z, ZIO E, et al. Condition assessment for the performance degradation of bearing based on a combinatorial feature extraction method[J] . Digital Signal Processing,2014,27:159 − 166. doi: 10.1016/j.dsp.2013.12.010 [13] REN L, SUN Y Q, WANG H, et al. Prediction of bearing remaining useful life with deep convolution neural network[J] . IEEE Access,2018,6:13041 − 13049. doi: 10.1109/ACCESS.2018.2804930 [14] WANG F, LIU X, DENG G, et al. Remaining life prediction method for rolling bearing based on the long short-term memory network[J] . Neural Processing Letters,2019,50(3):2437 − 2454. doi: 10.1007/s11063-019-10016-w [15] 孙鑫, 孙维堂. 基于多尺度卷积神经网络的轴承剩余寿命预测[J] . 组合机床与自动化加工技术,2020(10):168 − 171. [16] 张继冬, 邹益胜, 邓佳林, 等. 基于全卷积层神经网络的轴承剩余寿命预测[J] . 中国机械工程,2019,30(18):2231 − 2235. [17] HINCHI A Z, TKIOUAT M. Rolling element bearing remaining useful life estimation based on a convolutional long-short-term memory network[J] . Procedia Computer Science,2018,127:123 − 132. doi: 10.1016/j.procs.2018.01.106 [18] CHEN Y S, JIANG H L, LI C Y, et al. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks[J] . IEEE Transactions on Geoscience and Remote Sensing,2016,54(10):6232 − 6251. doi: 10.1109/TGRS.2016.2584107 [19] GREFF K, SRIVASTAVA R K, KOUTNIK J, et al. LSTM: A search space odyssey[J] . IEEE Transactions on Neural Networks and Learning Systems,2016,28(10):2222 − 2232. [20] ZOU F Q, ZHANG H F, SANG S T, et al. Bearing fault diagnosis based on combined multi-scale weighted entropy morphological filtering and Bi-LSTM[J] . Applied Intelligence,2021,51(10):6647 − 6664. doi: 10.1007/s10489-021-02229-1 [21] FRANCESCHI D, JANG J. Demystifying batch normalization: analysis of normalizing layer inputs in neural networks[C]//Proceedings of International Conference on Optimization and Learning. Cham: Springer, 2020, 1173: 49 − 57. [22] WANG Q B, ZHAO B, MA H B, et al. A method for rapidly evaluating reliability and predicting remaining useful life using two-dimensional convolutional neural network with signal conversion[J] . Journal of Mechanical Science and Technology,2019,33(6):2561 − 2571. doi: 10.1007/s12206-019-0504-x -






 下载:
下载: